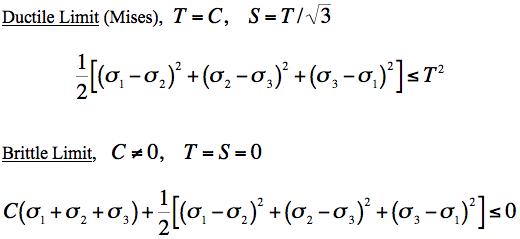Richard M. Christensen |
||
The Brittle Limit
There is not even agreement on what should constitute the brittle limit or if it even exists. In the two property, polynomial invariants method given here for homogeneous and isotropic materials, the uniaxial tensile and compressive strengths, T and C, are found such that the ductile limit is defined by T/C→1 while the brittle limit is defined by T/C→0. Some would say that the brittle limit so specified is only a mathematical abstraction and of no practical use or interest. Such is not the case. It is here argued that for any candidate failure criterion, it is very important to examine its behavior in the brittle limit as T/C→0 in order to determine whether reasonable and consistent results emerge, or if physically unacceptable or pathological results are obtained. In the latter case the supposed failure criterion should be discarded because with aberrant behavior at the limit it would be certain that the form could not have generality and would be of little or no value. For example, consider the two property Coulomb-Mohr failure criterion. In the brittle limit, T/C→0, the Coulomb-Mohr form allows all principal stresses that are negative (or zero) in value. This then implies that such a material has a uniaxial compressive strength that is of indeterminate size, even unlimited in magnitude. In effect no property is involved at the brittle limit, yet the material can support load. This clearly is an unphysical and unacceptable behavior, the Coulomb-Mohr failure criterion is degenerate at the brittle limit. This probably is the simplest way of revealing the general unacceptability of the Coulomb-Mohr criterion. Other examples of proposed but actually inadmissible failure forms will be given in the section: Critical Tests for Failure Criteria. As a counter example, consider the failure criterion developed in this website, and in papers before that. First by way of a little background, the Mises criterion has only one property. For a general two property failure theory that has the Mises criterion at its ductile limit, one might reasonably expect that its brittle limit would also turn out to be a one property form. As shown below exactly that does occur here. The governing equations for the present two property isotropic material failure criterion are given at Governing Equations. In the ductile and brittle limits and in terms of principle stresses these become
and
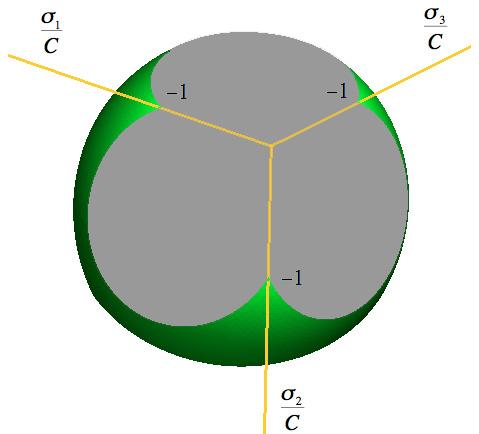
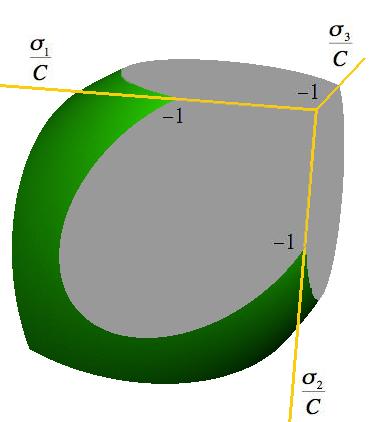
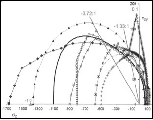
The brittle limit is shown below in three dimensional graphics forms. The coordinate axes are given in the negative stress directions. The general form of the failure surface is that of a triangular pyramid which transitions into a paraboloid with corners between the two.
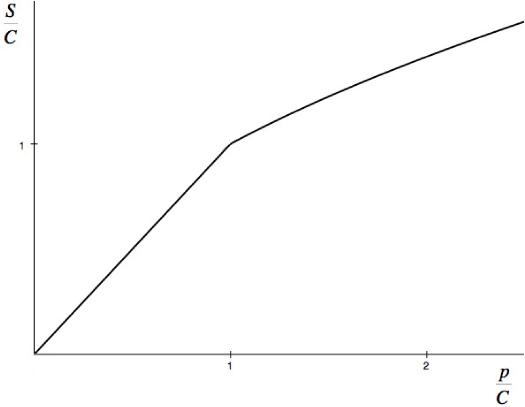
Taking σ3=0 gives the two dimensional biaxial stress failure envelope at the brittle limit as
It does not follow that the failure modes are necessarily brittle in these two dimensional and three dimensional examples. The large negative mean normal stresses have an influence on that situation. The significance of these results is that the brittle limit does not allow any tensile stresses at failure, in addition to the other primary features. The failure criteria at the brittle limit show that the shear strength, S, must vanish. However, if a state of pressure, p, is applied first, then some shear strength should become possible, as a superimposed stress state. This is found to be true here, with the shear strength dependence on the pre-applied pressure as shown below.
These examples and results demonstrate that a well founded, three dimensional failure theory can and must evoke consistent behavior at the brittle limit. The explicit physical form of the brittle limit also is of special interest in its own right.
|
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
Recent Additons |
||||||||||||||||||||||||||||||||||||||||||||
Key Junctures |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
General Matters |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
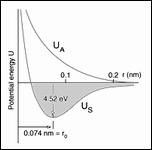
Can Atomic/Nano Scale |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
Copyright© 2019 |
||||||||||||||||||||||||||||||||||||||||||||
 There are unlimited numbers of two (or more) parameter failure criteria forms that must be considered, even just for isotropic materials. The first logical step in discriminating among the many possible forms would be to examine their limiting cases. The ductile limit is easy and obvious, most would agree that it must be the Mises criterion while the remainder might prefer the Tresca criterion. Between these two long standing forms the ductile limit case is covered. However, the situation with the brittle limit is historically completely opaque.
There are unlimited numbers of two (or more) parameter failure criteria forms that must be considered, even just for isotropic materials. The first logical step in discriminating among the many possible forms would be to examine their limiting cases. The ductile limit is easy and obvious, most would agree that it must be the Mises criterion while the remainder might prefer the Tresca criterion. Between these two long standing forms the ductile limit case is covered. However, the situation with the brittle limit is historically completely opaque.