Richard M. Christensen |
||
|
||||
Recent Additons |
||||||
Key Junctures |
||
 |
||||
General Matters |
||||
 |
||||
 |
||||||||
 |
||||||||
 |
||||||||
 |
||||||||
Can Atomic/Nano Scale |
||||||||
 |
||||||
 |
||||||
 |
||||||
 |
||||||
 |
||||||||
 |
||||||||
 |
||||||
 |
||||||
 |
||||||||
 |
||||||||
 |
||||||
Copyright© 2019 |
||||||
Letter to World Wide Failure Exercise, WWFE-II
 In the early 1990’s a program was begun to evaluate failure criteria for fiber composite materials. This “World Wide Failure Exercise” was conceived and conducted by M. J. Hinton and A. S. Kaddour and others. It functioned for over a decade and involved the participation of many advocates for many different possible approaches to the problem. The end results were largely inconclusive. This probably was not the fault of the failure exercise itself, but more likely reflected the disorganized state of the field and the difficulty of the problem.
In the early 1990’s a program was begun to evaluate failure criteria for fiber composite materials. This “World Wide Failure Exercise” was conceived and conducted by M. J. Hinton and A. S. Kaddour and others. It functioned for over a decade and involved the participation of many advocates for many different possible approaches to the problem. The end results were largely inconclusive. This probably was not the fault of the failure exercise itself, but more likely reflected the disorganized state of the field and the difficulty of the problem.
In recent years a second World Wide Failure Exercise has been initiated, again with the same organizers and with many participants. A few months ago the first results from this second effort were published. After that formal disclosure, the letter below was sent to Drs. Hinton and Kaddour by e-mail on November 20, 2012. It contains some observations, reactions, and suggestions, all intimately related to failure criteria for fiber composites in general, and to the WWFE-II in particular.
November 20, 2012
Dr. M. J. Hinton
Dr. A. S. Kaddour
World Wide Failure Exercise
Dear Mike and Sam,
I see that the WWFE-II is starting to be published. It will be an interesting and helpful contribution. There must be a great many different threads to coordinate and follow through. I’m sure you would appreciate some feedback if something not quite right slips through. This letter concerns one such correction.
In your Part A, in J. Comp Mats., Vol. 46, Nos. 19-20, page 2632, September 2012, you make reference to what you call the “Christensen theory” and give a preliminary evaluation of it as follows:
“Similarly, Christensen’s theory gave some of the lowest predictions in test cases 2, 3, 5-8. ---------- These were the result of the use of a single second order quadratic failure criterion for the matrix and the assumptions made regarding the relationship between the through-thickness shear strength and the transverse tension and compression strength of a lamina. ------------“
That statement is not correct. In fact it states the circumstances completely backwards. The predictions shown do not use what you call an assumption relating S23 to T22 and C22. On the contrary, the results shown are the deficient and unsatisfactory predictions obtained by not using a better calibration on S23. Let me explain this as carefully as possible, bearing in mind that nothing connected with failure theory is simple or obvious, in anyone’s theory. That is probably the one thing upon which everyone can agree.
I imagine you also might appreciate hearing a little more about this particular failure theory since I am not part of or directly involved with the failure exercise. Before getting into that, I salute your apparent intention to assess how any particular failure criterion actually functions and where it comes from. The theoretical foundations of a given failure criterion are almost as important in trying to assess its likely generality as are the comparisons with some data sets that are themselves very difficult to generate.
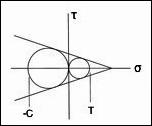
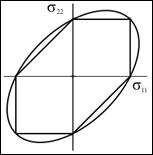
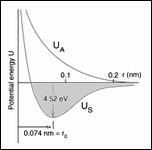
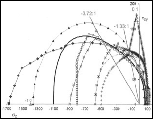
The first part of my theory of failure for aligned fiber composites treats the transverse strength properties S23, T22, and C22 as being independent. But it was found that there is an upper limit and a lower limit on S23 relative to the other two properties. At S23 squared = (1/4)T22C22 a lower limit is obtained because at values smaller than that for S23 the failure theory switches over to giving an open failure envelope rather than the necessarily closed envelope for stress states with Sigma 22 vs. Sigma 33. On the other hand when the composite material reverts to being entirely the homogeneous and isotropic matrix material it is found that S23 squared = (1/3) T22C22 and this is an upper bound for S23. Thus S23 must fall between these two close values. A micromechanics derivation was used to give an explicit relation for S23 in terms of T22C22 and it is between these bounds. But this is a subsidiary result and it does not really answer the basic question of what is actually happening here, even though it has practical use and value.
The answer to the underlying relationship between S23, T22, and C22 is simple, revealing, and completely utilitarian. It is as follows. Take P22 as being the failure stress under eqi-biaxial transverse compressive stresses. For given values of T22 and C22 the failure theory predicts that failure stress P22 is extremely sensitive to small changes in S23. On the other hand, when the roles of the two failure stresses are reversed, then the failure stress S23 is found to be very insensitive to changes in specified P22. This is just elementary sensitivity analysis but it is vital to understanding the failure behavior.
The bottom line then is this. The transverse pressure to fail the fiber composite is much, much larger than the transverse shear stress to fail the composite. The permissible range for P22 is huge. The transverse shear strength S23 acts as a conjugate to P22, and it has an extremely narrow range of acceptable values. The micromechanics analysis accordingly was used to solve for S23 in terms of T22 and C22. It is given by S23 squared = (2/7)T22C22. This result is at T22/C22 = 1/3, the usual level for carbon-epoxy systems. Current work aims to find a more general form, valid for all values of T22/C22.
This basic micromechanics result for S23 in terms of T22C22 should be used in all applications of the theory. The only exception would be if the transverse shear strength under very high pressure were used to determine S23 directly from data or, best of all, determined directly from data on P22. But those are exceedingly difficult experiments that never could and never would be done on a routine basis. Determining S23 by itself at zero pressure would be hopelessly inaccurate within the required limits of its behavior. The micromechanics result for S23 resolves the difficulty in treating these inherent and deeply embedded characteristics of fiber composites failure.
Another completely different facet of transverse failure behavior is also important. The transverse matrix controlled failure criterion of this failure theory is that of a single form. Many or most other transverse failure criteria take forms having multiple branches. It is often said that multiple forms are necessary. The point of view here is exactly the opposite of that. A quadratic form that accommodates both tensile and compressive failure stresses is a very strong indicator that a single, comprehensive failure form may be possible. In contrast, the imposed use of multiple forms is a tacit presumption that it is not possible to have a single, comprehensive form and it is necessary to fall back upon a “fitting operation” involving multiple forms.
When Part B of WWFE-II is put together I trust that it will clear up the mis-understanding on what is what in this failure theory. Of course I can’t say how this theory will do compared with the other theories, but I can say with complete and utmost confidence that it will do far better than did the incorrect form of it used in Part A.
Probably all of this is best understood and appreciated in its connection with isotropic material failure theory. It is very hard to imagine getting fiber composites failure right if you first don’t have isotropic materials failure absolutely nailed down. In isotropic theory it is found that S squared = (1/3)TC. But if that were to be ignored and the shear strength S were blindly taken to be independent of the uniaxial strengths T and C it would then be found that the predictions in high pressure stress states would be extremely sensitive to the reported values for S. As a consequence the experimental scatter in the S values would give some peculiar and bizarre failure predictions from the theory. That approach would be a complete dead end for isotropic materials failure.
The situation with the transverse failure properties in transversely isotropic materials is, not surprisingly, very similar. The S23 property cannot be taken to have unlimited variation. It has a very narrow window of values over which it is consistent and allowable with the other properties. It is essential to understand what is independent and what is not, and what has great sensitivity and what does not in any particular theory. Physics is full of such examples. The classical example is the relation between range and angle of inclination in ballistics. Most high definition theories have such trade offs. As a matter of fact, boundary layer theory for aligned fiber composites is almost exactly that same situation, scale is everything. In the present context, it all comes together when approached in this manner.
Now with the above understanding, the following can be said. It would be physically unrealistic and completely misleading to expect that S23 could be independent of T22 and C22 for transversely isotropic (fiber composite) materials, especially when for three dimensionally isotropic materials S is indisputably and exactly determined by T and C. After all, two dimensional isotropy and three dimensional isotropy are closely related. The explicit micromechanics relation between S23 and T22 and C22 is a powerful new result revealing a basic aspect of fiber composite materials behavior.
The status of this particular theory for unidirectional fiber composites failure is as follows. This theory for anisotropic composites is the generalization of the polynomial invariants derivation for homogeneous and isotropic materials. The latter failure theory has a solid derivation and verification for isotropic materials, including metals, polymers, ceramics, glasses, and geological materials. The anisotropic composites failure form is not a far out conjecture or some patched together fabric of a few failure modes. It is the most direct generalization of the isotropic field theory of failure. Please see the reference at the end of this letter.
In other but related matters, let me add a couple of small suggestions that might be helpful to the WWFE process or at least be worth considering. The lamina level failure theories naturally separate into two groups and perhaps could first be compared and evaluated within their own group:
(i) Primarily macro-mechanics developed
(ii) Primarily micromechanics developed
My work falls under group (i) even though it has important backup from micromechanics. Each is a legitimate general approach and there are pros and cons to each. Who knows how it all will play out in the end. Assessing each group separately would give a balanced format at this point in time. Perhaps there could also be a final comparison between the most useful ones from the two such fundamentally different approaches.
Additionally, it would be very helpful to have the participants specify how many parameters are required to fully calibrate their failure theory. For example, my failure theory requires and is completely specified by 5 properties, the strength properties T11, C11, T22, C22, and S12. Further, they should give a brief glossary of the needed properties and parameters. This Glossary of Input for each theory would be of tremendous help to the community of possible users.
It is obvious that you expend great effort in documenting all matters related to the failure exercise. In this connection, please include this letter in any published discussion forms and records. Treat this as a letter to the editor, which is what it is. Also, I don’t mind if you forward this letter to all the participants in the failure exercise, openness benefits everyone.
Although not a participant myself, I necessarily have a considerable interest since my work is formally involved. Understandably I want to see it be correctly and properly applied, as I’m sure do all of the active participants and as do you. Indeed, whether as a direct participant or not, we all have a vested interest in supporting a deep and complete and exhaustive failure exercise that can finally show some progress in the field.
Reference: The Theory of Materials Failure, R. M. Christensen, Oxford University Press, publication in early 2013.
Dick
Richard Christensen
Richard M. Christensen
February 10, 2013



