Richard M. Christensen |
||
Can Atomic/Nano Scale Failure Events Predict Macroscopic Failure
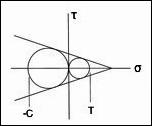
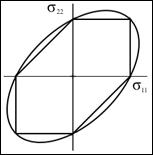
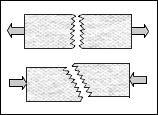
From a purely macroscopic stress point of view the apparent problem is of immense size. For three dimensional conditions there are six independent components of stress, three of which have sign dependence. Also, account must be given for the possible interactive combinations of these variables. Furthermore, account must also be given for nonlinear dependencies, linear forms are not sufficient. The possible combinations of all these effects are almost unlimited. A carefully organized attack on the problem is necessary and unthinkable otherwise. The synthesis of all these failure causative effects as being derivative from a few basic atomic or molecular (nano scale) properties would seem to be compelling. However, the formation of macroscopic failure criteria from atomic/nano scale effects must be quantitative and discriminating. Qualitative or comparative projections have no meaning for failure criteria. Going a step further, an appealing approach would be to use molecular dynamics (or some variation of it) to signify failure when an atomic bond(s) is stretched or distorted beyond its limit. This then presumes that molecular scale failure is predictive of macroscopic failure. However, some examples to be considered next suggest that the problem is far more complex than this direct approach would imply. The Peierls-Nabarro theory for the stress necessary to move a single dislocation is very well posed and elegantly executed. But, it is several orders of magnitude different from reality. Nevertheless it remains a landmark result for an extremely difficult problem. It can be said that this is a theoretical result, what about basing conclusions on direct observations. Experiments show that dislocation flow can be detected at extremely small stress levels, virtually from the beginning of loading, thus not giving any useful information for the present quandary. In another example, fracture mechanics when first conceived by Griffith was thought to be completely specified by the atomic scale surface energy due to broken bonds (along with modulus and crack size). This too was found to be many orders of magnitude wide of the mark. Finally, for a third, completely different example, the compressive strength for aligned fiber composites is limited by the unstable formation of kink bands. These kink bands involve cooperative motions between the fiber phase and the matrix phase at scales enormously larger than those of atomic/nano dimensions. Failure examples such as those just described effectively indicate that there is an operative principle or imperative that dictates that any particular failure mode has its own identifiable scale or range of scale of occurrence. It follows that damage/failure events at much smaller scales as well as events at much larger scales are of no relevance to the controlling range of interest. An extreme example of scale dependence and mismatch is as follows. One would never use molecular dynamics to predict the buckling of stringers in aircraft. Examples such as this can quickly be dismissed as illegitimately bridging over from extremely fine scale materials failure to structural failure. It is easy to separate these two failure types in this particular example, but they may be much less easy to separate in other cases. Situations can arise where two hypothetical failure modes are close, at least in an order of magnitude sense, and somewhat difficult to distinguish. The guiding rule is to treat each and every failure mode at/in its own scale range of occurrence. Continuing with the scale question, it is not possible to unilaterally and arbitrarily assign the scale for macroscopic failure characterization. The physical failure mechanism itself dictates the operative scale of its emergence and its overriding control. This occurrence also necessarily depends upon the scale of the problem. The usual uniqueness associated with linearity gives way to the nonlinear bifurcation of failure. In general, many different failure mechanisms can compete for dominance within a given range. This discussion certainly does not negate the usefulness of studying failure at very small scales: quantum (mechanics), angstrom, nano or thereabouts. Research at those pre-selected scales (and at all extremely small scales through multi-scale modeling) has a highly useful and important role to play in providing new insights, possibly leading to improvements in the chemical composition of materials or even to entirely new materials. In strong contrast, it is necessary that the failure criteria that are to be used to certify actual designs be carefully calibrated to the scale measures of the intended application. In other words, modeling failure at the atomic scale and modeling failure at the macroscopic scale are two distinctly different and largely independent endeavors with much different consequences. It is very important that they not be treated jointly with one somehow thought to be predictive of the other. To do so could be seriously misleading for either purpose. The term failure criteria as used herein will always connote macroscopic conditions associated with the idealization of homogeneous materials. In this approach all flaws and imperfections that exist at scales below that of the homogenization process are implicitly and automatically involved in calibrating the materials strength performance and in establishing the related general characteristics. In most cases it is the defect structure, which itself can be scattered across many scales, that interacts with the intrinsic atomic scale properties to determine the three dimensional strength of the material. This interaction is deeply faceted and complex, generally requiring that macroscopic failure criteria be treated as an independent area of research and application. When properly developed, the macroscopic scale approach can be as rigorous and incisive as that at any scale. Finally, it should again be emphasized that there are great benefits to be gained from studies of materials failure at all scales. A balanced view is that a physical understanding is needed at all scales independently, no one scale can satisfy all needs. While quantitative transport of properties across many orders of magnitude of scale is a noble objective, it is not usually realistic within the failure realm. However, qualitative projections across scales can often applied to considerable advantage, but that is a separate topic.
|
|||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
Recent Additons |
|||||||||||||||||||||||||||||||||||||||||
Key Junctures |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
General Matters |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
Can Atomic/Nano Scale |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||
 |
||||||
Copyright© 2019 |
||||||
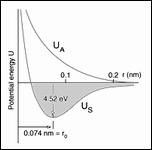
 The tremendous success for predicting elastic stiffness properties (and other transport properties) from atomic scale modeling suggests doing the same thing for the strength properties of materials. The attraction of doing this is that a minimal number of “fundamental” atomic scale failure properties could then be used to form failure criteria that in turn could predict failure for any macroscopic state of stress.
The tremendous success for predicting elastic stiffness properties (and other transport properties) from atomic scale modeling suggests doing the same thing for the strength properties of materials. The attraction of doing this is that a minimal number of “fundamental” atomic scale failure properties could then be used to form failure criteria that in turn could predict failure for any macroscopic state of stress.


