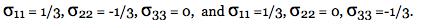Richard M. Christensen |
||
The Ductile-Brittle Problem
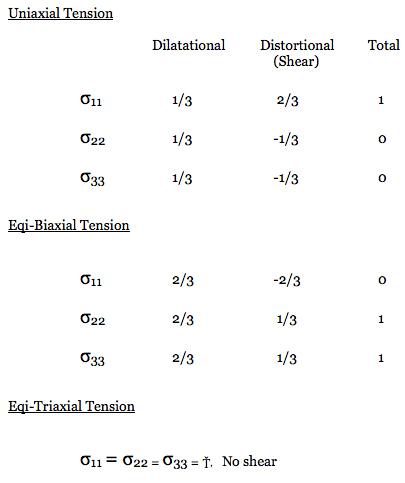
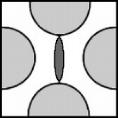
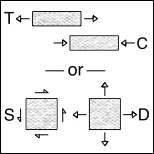
Some perspective on the problem can be gained as follows. The same as with temperature, pressure can be used to control ductile-brittle effects. Sufficiently large superimposed pressure can convert what is normally thought of as a brittle material into a ductile material. Bridgeman was awarded the Nobel Prize at least partially for illuminating the problem nearly a hundred years ago. However, positive or negative pressures are but a part of the full stress tensor, and because of this they are more complex than scalar temperature variation. This complexity has been something of a barrier to the understanding of ductile-brittle failure effects. Proceeding further with this ductile-brittle reconnaissance, all stress states can be decomposed into a dilatational part (as with hydrostatic stress) and a distortional part (as with shear stress). Consider the three following stress states, uniaxial tension, eqi-biaxial tension, and eqi-triaxial tension. The decomposition of these stress states into dilatational and distortional parts are as shown in the table below.
Each of the two distortional (shear) stress states can be further decomposed into two simple shear stress states as with
For further investigation, consider only those materials that are normally thought of as being very ductile, e. g. aluminum, copper, etc. Such isotropic materials have the uniaxial tensile and compressive yield stresses as being identical, T = C, to within experimental discrimination. Also, the same failure values occur for eqi-biaxial tension, for these materials. Other materials types have T/C<1, or much less in some cases. For convenience, refer to the distortional part of the stress tensor as shear. Designate by S a measure of the shear part of the stress tensor (the Mises stress for example) and by D designate a measure of the dilatational part, both at yield/failure. Normally it is only the shear part that controls yield/failure in these T = C materials but it is both S and D that relate to the ductile versus brittle failure mode type. For present purposes, take a possible ductility index for these three cases as specified by S/D. In the uniaxial tension case normalize this S/D ratio to the value of 1. It then follows that the S/D ratio for the eqi-biaxial tension case will have the value of 1/2 because it has the same value for S as in uniaxial tension (the sign change shown in the table is irrelevant) but its value for D is twice as large as that in uniaxial tension. Finally, for the eqi-triaxial tension case there is no shear, S = 0, so its ductility index is S/D = 0. In this manner and for these three cases there is a ductility scale that goes from 0 to 1 with the value 0 being that of no ductility (major brittleness) and that of 1 being major ductility. Collecting these three cases for materials with T = C then gives
The triaxial case falls into the brittle category since there are no shear stresses to activate dislocation flow in these T = C materials. That an eqi-triaxial tension test is exceedingly difficult to perform is not of concern here, only the type of failure is being considered. The present reasoning and discussion is for background purposes only and does not represent a specific technical approach. Nevertheless it does quite clearly indicate that there is a primary linkage between (i) ductile versus brittle failure behavior and (ii) the type of stress state which is imposed. Any comprehensive failure theory must account for these effects. They can be just as important as the effects due to temperature variation. They comprise the litmus tests (criteria) indicating and differentiating ductile yield behavior from brittle failure behavior. A general criterion for the ductile-brittle transition is developed in a published paper (2005) which is listed and can be downloaded in Section II of this website. The theory given there interestingly determines that the state of eqi-biaxial tension for materials with T = C does infact lie on the borderline transition between ductile yield and brittle failure. More importantly, the theory covers all isotropic materials types having T ≤ C, and all stress states. |
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
Recent Additons |
||||||||||||||||||||||||||||||||||||||||||||
Key Junctures |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
General Matters |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
Can Atomic/Nano Scale |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||
Copyright© 2019 |
||||||||||||||||||||||||||||||||||||||||||||

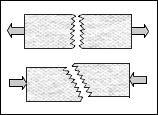
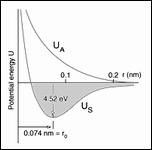
 The distinction between ductile failure and brittle failure is one of the cornerstones of materials science, in addition to being of utmost importance for materials applications. Ductile-brittle transitions as influenced by some control variable, such as temperature, have been very extensively examined. Basic theoretical studies of the transition effect have usually (but not always) been posed in the context of the activation and flow of atomic scale dislocations in face centered cubic and body centered cubic metals, or in more idealized forms. Despite the large amount of research already done on the ductile-brittle transition, very little of it has been successfully reduced to standard practice and a uniformity of understanding for the full spectrum of materials types. The specification of ductile versus brittle failure criteria for all homogeneous materials has continued to be indistinct and elusive.
The distinction between ductile failure and brittle failure is one of the cornerstones of materials science, in addition to being of utmost importance for materials applications. Ductile-brittle transitions as influenced by some control variable, such as temperature, have been very extensively examined. Basic theoretical studies of the transition effect have usually (but not always) been posed in the context of the activation and flow of atomic scale dislocations in face centered cubic and body centered cubic metals, or in more idealized forms. Despite the large amount of research already done on the ductile-brittle transition, very little of it has been successfully reduced to standard practice and a uniformity of understanding for the full spectrum of materials types. The specification of ductile versus brittle failure criteria for all homogeneous materials has continued to be indistinct and elusive.