Unsolved Problems

 

The term unsolved problems does not refer to particular applications that have not yet been addressed. Rather, it means gaps in understanding for the basic formulation of failure criteria. There are major openings for further work and for entirely new work on the many different aspects of the theory and its means of application. A short list has been composed for some of the problems of significant opportunity in the field of failure criteria.

Many of the items on this list are related to matters under discussion in this website, and thereby in the seven archive papers on which the website is based. The list is far from being exhaustive or even comprehensive. It is more like a sampling of possible problem areas in moving forward. No attempt is made to go into details on any of these areas, but they should convey the kernels of the problems. Some problems may be rather easy, they simply have not yet come to the surface. Others may be extremely difficult or even defy solution.

The problems will not be listed in any particular order. It would require much more information to attempt any classification based on such matters as sub-topics, physical relevance, general importance, scale of difficulty, or even just isotropic versus fiber composites. There is much commonality of problems over many areas. The list may be appended, fine tuned, or even considerably changed in the future as further work is added to the website.

Before getting into the list, a very brief account will be given of the formative developments in the field of failure criteria. This provides the obvious prelude to further activities in general, and to the problems list in particular.

Although failure criteria have been around since the beginning of mechanics of materials, it has only been within the past many years that it has become more than just a casual speculation. In this regard, there are interesting parallels and contrasts between the respective developments of failure criteria and fracture mechanics. Griffith launched fracture mechanics in the 1920’s. In about the same time frame, Mohr took Coulomb’s original concept of failure and put it into an appealing and usable form, the Mohr-Coulomb or Coulomb-Mohr criterion. So both efforts, failure criteria and fracture mechanics, effectively commenced almost simultaneously.

Griffith’s approach to fracture languished for several decades before being revitalized and activated. In contrast, almost immediately there was high promise and even excitement for the Coulomb-Mohr theory. So much for short term promise! The Coulomb-Mohr criterion gradually faded into the background as being only a historical artifact. It completely failed to show relevance for a wide range of isotropic materials. Fracture mechanics on the other hand eventually matured into the complete and active field that it is now. There matters stood until comparatively recent times. It is only in the past few decades that failure criteria have returned to prominence and serious activity.

So in reality, failure criteria is a young technical enterprise. It is much younger in a developmental sense than the now mature fracture mechanics field. When one says “fracture mechanics” there is absolutely no question as to the exact and explicit governing discipline. See Section VIII for the outline of fracture mechanics and the distinction between it and failure criteria. When one says “failure criteria” a broad range of possible images can easily come to mind. There are in circulation a great many empirical formulas of uncertain validity but they all still fall under a broad subject heading of failure criteria.

However, the terminology “failure criteria” and “failure criteria field” is used here in a much more restrictive and specific sense. Here failure criteria will usually refer to forms that have a significant theoretical basis for their existence and a physical compatibility with quality testing data, when such data exists. Ideal though this may seem, making judgments consistent with this objective are just about guaranteed to generate controversy. Such is the nature of developing fields.

Let it finally be said that the failure criteria field is and must remain wide open to new ideas and new approaches. Much more can be expected from an active and thoughtful community. Here now is the qualified list of unsolved problems for failure criteria. Comments and suggestions are welcome.

 

---

Should failure criteria be treated as part of the constitutive formulation for the material? That is the direction followed here. Are there any contradictions in this approach? If so, how should failure criteria be viewed as fitting into the overall formulation for materials?
 

---

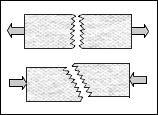
Spallation type failure due to pressure wave reflection is a common occurrence in impact and detonation problems. Even very ductile materials undergo spallation. Can this be related to ductile versus brittle failure behavior as determined by the stress state type? More specifically, can the ductile/brittle criterion of Section VII be applied to this problem?
 

---

Can failure criteria be formulated as a variational theory formalism? There has been some initial work in this direction, particularly for fracture mechanics. Can this approach be brought to a utilitarian level of application for failure criteria?
 

---

Delamination in composite material laminates is an especially active and important area. Cohesive zone failure models are often used, especially with numerical modeling. When do these models best apply, and when do regular failure criteria best apply to delamination problems?
 

---

The following criterion for the ductile/brittle transition is given in Section VII

where I₁ is the first invariant in terms of the failure stresses. In the limit of a perfectly ductile material, T/C=1, the criterion divides the Mises yield cylinder in principal stress space into ductile and brittle regions as

 

 

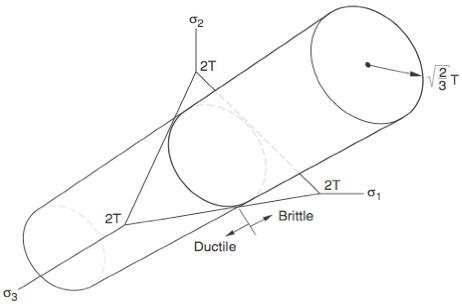
Thus a sufficiently large superimposed tensile state is predicted to convert a normally perfectly ductile metal into a brittle material form. This cannot be explained through conventional dislocation theory. What modification to the theory would be needed to explain this? Can the Rice-Thomson theory of the ductile/brittle transition be applied or modified to apply to this problem? Would the explanation necessarily require a dislocation core incorporation?
 

---

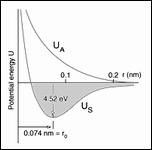
The present failure theory for isotropy is for macroscopic field theory applications. It is calibrated by uniaxial T and C. Can these two macroscopic strength properties be expressed in terms of nano or micro scale variables to generate a nano (or micro) theory of macroscopic strength?
 

---

One of the likely future opportunities is in the area of very large scale computations and information technology (IT). This is quite different from posing a single, idealized and isolated boundary value problem and then seeking the related unique limit of strength performance. Probably strength characterization will be used in ways not yet imagined but it is almost certain that IT will contain strength sub-routines in some form or other. It is far better that this be based on realistic information rather than just on anecdotal evidence. Perhaps the IT uses of failure criteria for materials could relate to the problem area immediately preceding this one.
 

---

A common approach for the use of ceramic materials is simply to avoid all applications involving tensile stress components. How can a more rational approach be devised through using failure criteria but as specialized to ceramics and other similar materials?
 

---

This website provides a two property failure criterion for isotropic materials. The only other general purpose two property forms are the Coulomb-Mohr criterion and the Drucker-Prager criterion. All other general forms that have been proposed involve three or more parameters. A contrary point of view would be that a two property form is impossible. Is there a proof of this or can a fundamental contradiction be constructed?
 

---

For isotropic materials a comprehensive treatment of ductile versus brittle failure behavior has been developed. Are similarly general ductile versus brittle developments possible for fiber composite materials? If general developments are not forthcoming, at least could the transverse tensile and fiber direction tensile strengths admit a ductile versus brittle criterion? Their D/B behaviors presently are rationalized only on an intuitive basis!
 

---

There are many molecular level theories for amorphous or crosslinked, glassy polymers. Generally they involve many parameters to reflect a variety of features in molecular scale architecture and bonding. How can these usefully be related to a two property macroscopic level failure criterion?
 

---

The present treatment of failure criteria as well as most treatments are of a time independent nature. How should elasticity (time independent) type failure criteria be modified to incorporate time dependent, viscoelastic effects? How does creep rupture fit in with these categories?
 

---

All ductile/brittle matters are of high relevance and importance. A method of predicting ductile versus brittle failure behavior has been given here as related to the materials type (T/C ratio) and the imposed stress state. Is there a completely different macroscopic D/B approach that could be taken to achieve the same objective? Could ductile versus brittle behavior be quantitatively related to or correlated with other physical specifications such as some of the thermo-mechanical properties?
 

---

Testing the validity of failure theories for fiber composites are under investigation in the World-Wide Failure Exercise (WWFE), M. J. Hinton, A. S. Kaddour, and P. D. Soden, Elsevier, 2004. This large scale evaluation program focuses upon the most difficult problems related to the load carrying capabilities of fiber composites. Any current activities of this type should be compared with and correlated with the past, present, and future investigations in the WWFE. Are there any means and mechanisms for assimilating all the fragmentary evidence already in existence, some real and some little more than hearsay?
 

---

Dislocation theory predicts that resolved shear stress leads to the Tresca criterion. Macroscopic material behavior shows that the Mises criterion is the more proper form. Although there have been explanations for this divergence they are not completely convincing. Is there an all inclusive explanation, perhaps involving the effects at grain boundaries?
 

---

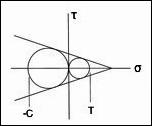
Relative to the present theory of failure, the brittle limit has been extracted in mathematical form in the section The Brittle Limit. In principal stress space the failure form is given by

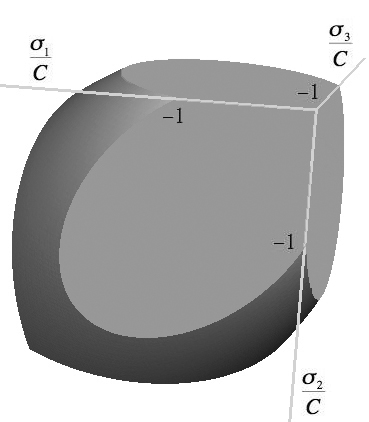
Can a physical model involving damage patterns be reasoned to represent this case? If not in three dimensions, can it be done in two dimensions?
 

---

Although the Coulomb-Mohr theory has no credibility for cohesive engineering materials it remains as a useful form for soil mechanics and some granular materials. It is the most credible two property (parameter) form for these latter types of flow. Is there any relationship between soil mechanics and the cohesive engineering materials classes, or are they irretrievably separate and distinct?
 

---

How should yield stress and failure stress be defined? Traditional methods are quite arbitrary. A future section will be added here on this subject, but no doubt other approaches may also be appropriate. Will there ever be unique definitions for these?
 

---

A specific criterion for the ductile-brittle transitions has been derived in Section VII. Does this have any relationship to a second order transition as is often posed in thermodynamical terms?
 

---

There is a great need for critical experiments that test failure criteria in new and original ways. Difficult and expensive though such testing may be, it must remain as a prime objective. What should be the most important guidelines and objectives to be investigated in the testing?
 

---

Typical failure criteria approaches focus upon a specific class of materials, such as ductile metals, or brittle metals or polymers etc. They then fit parameters to data for specific stress states. Can such empirical approaches be taken to apply for other stress states if they do not apply across the various materials classes and certify generality in that way?
 

---

A long standing problem is that of “in-situ” strength properties versus “virgin” material properties. This is particularly important with fiber composites although it is common to all materials applications. How should failure criteria be modified, if at all, to reflect these effects?
 

---

The existence of significant linear elastic ranges of behavior in engineering materials is an extremely fortunate but rather poorly understood phenomenon. For example, in ductile metals, dislocation emission occurs upon the first small increment of load application but at some point the rate of emissions multiplies hugely and cascades into macroscopic yield/failure. Many other materials types show similarly sudden changes in behavior with load application. What are the underlying physical mechanisms that cause such abrupt changes in constitutive behavior? Can some or most cases be explained by localization or is every different materials type explained by a different mechanism?
 

---

Do failure criteria have a place and use for materials that have no effectively linear elastic range of behavior?
 

---

The failure theories in this website involve surfaces in stress space that include intersections (corners). These result from the competition between failure modes. To what extent do these corners reflect reality or are they just acceptable idealizations? Are acute angle intersections less likely than wider range angle ones?
 

---

Can nanoscale indentation be used to critically assess failure criteria?
 

---

Some aligned fiber, composite material failure theories are explicitly expressed separately in terms of tensile failure modes and compressive failure modes. The present general failure theory for aligned fiber composites does not require degeneration and separate specification in tensile and compressive modes. Its quadratic form automatically yields the tensile and compressive modes, in the same way as for isotropy. Are there any contradictions between the two different approaches?
 

---

The basic question continues as to whether stress or strain is the appropriate variable for failure criteria. A rationale for stress has been give here. What are the other supporting arguments for stress and what are the arguments for using strain. Can either be reasoned to be truly fundamental?
 

---

The failure criteria derived here are implicitly intended for application with materials that either fail brittlely or show strain hardening. Is there any reason why these failure criteria cannot also be applied to materials that show strain softening, providing the failure state is suitably identified?
 

---

Relative to any particular symmetry class is there a relationship between the number of independent elastic properties and the number of independent failure properties? For isotropy there are two of each according to the methods given here. How do fiber composites compare in this regard?
 

---

The effect of superimposed pressure upon failure is in need of a comprehensive and critical treatment for isotropic materials. The present failure theory predicts that shear stress with pressure gives the failure envelope as

where p is the pressure. This relation must be supplemented by the fracture mode requirement

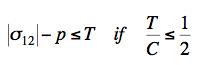
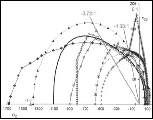
Other stress states admit similar forms. Predictions such as these can be compared with the famous Bridgeman data. In so doing, the efficacy of this quite old data must be assessed.
 

---

In fields with stress gradients, over what range can point specific failure criteria be applied? Is it possible to use point specific criteria over a region? If so, what would be the scale of the region and how would it relate to the stress gradient?
 

---

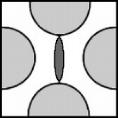
The problem of an isotropic thin sheet under uniaxial stress and containing a circular hole has a stress concentration factor of 3. There is no need for a separate failure criterion, the stress concentration factor is the failure criterion! This is because only a single component of stress is active. How many ideal strength problems of this type are there in existence?
 

---

How can the type of failure criteria derived and used here be modified to accommodate thermal stresses and residual stresses? Are there any thermodynamical insights to be brought to bear on these problems?
 

---

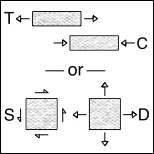
The two property failure theory developed here for isotropy has its calibration from T and C, the two uniaxial strengths. Can a two property theory be developed in terms of S and D, the shear strength and the positive dilatational strength? It should be noted that the present T and C theory cannot be converted to an S and D form because S and D forms cannot give the fracture criterion present in the T and C theory. Does this preclude a S and D theory?
 

---

Consider the problem of ideal, intrinsic strength properties. Can the intrinsic strength properties, which would ideally exist if there were no damage, defects or disorder, be predicted or inferred from strength measurements on existing materials? This would necessarily be limited to the mechanics of materials formulations. This would not be comprehensive from a general materials point of view. Is that a problem?
 

---