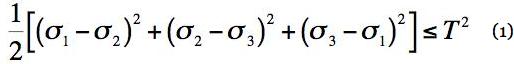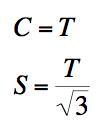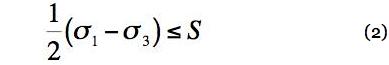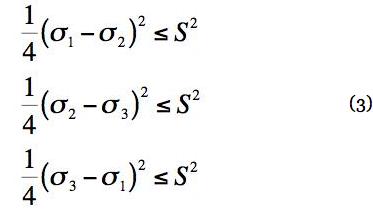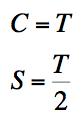Mises Criterion & Tresca Criterion


	Richard M. Christensen Brief Biography

How Do Mises and Tresca Fit In

FrontPageMisesTrescaGraph All mechanics of materials books have sections on strength and failure criteria. Usually the Mises and Tresca criteria are presented jointly with little discrimination or recommendation between them. What is more, often little else in the way of failure criteria are presented and the non-expert reader can be left with the impression that these two criteria cover all or nearly all materials, and it doesn’t greatly matter which one is used. Some books even grant these two criteria the status of being classical results. A general question to be posed here is this, can either or both of these criteria be considered to be classical results or are they merely long standing, comfortable forms but of no special distinction.

This website has made several references to the Mises criterion while the Tresca criterion has barely been mentioned. In this side section a careful look is taken of the two criteria, mainly in comparison with each other to see if there should be some inherent preference, even at this level. Concurrently, some observations will be given of how each fits into the larger picture involving generality beyond just that of the usual ductile metals.

The main interpretation of the Mises criterion is that it represents a critical value of the distortional energy stored in the isotropic material while the Tresca criterion is that of a critical value of the maximum shear stress in the isotropic material. Historically, the Tresca form was considered to be the more fundamental of the two, but the Mises form was seen as an appealing, mathematically convenient approximation to it. Now, both are usually stated side by side with little or no preference.

The two criteria are specified below in principal stress space. Both are one parameter forms, specified by either the uniaxial tensile strength, T, or the shear strength, S.

Mises Criterion, Critical Distortional Energy

equation1

where

equation2

Tresca Criterion, Critical Shear Stress

For the principal stresses ordered as σ₁ ≥ σ₂ ≥ σ₃ then

equation3

For the principal stresses not ordered

equation4

where

equation5

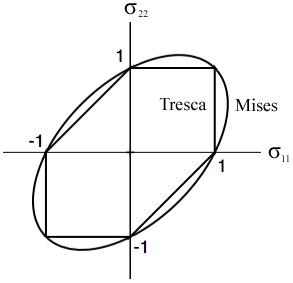
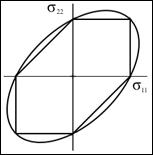
The three separate forms in (3) are for the maximum shear stresses in the three principal planes.

Both of these single parameter criteria can be calibrated on either T or S. The figures below, for biaxial stress states, calibrates both criteria on T and then on S.

Case I, Calibration on T

Graph1

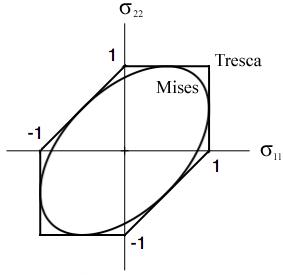
Case II, Calibration on S

Graph2

The maximum difference between the Mises and Tresca forms for both Cases I and II is 14.4%. The essential and striking differences between the two are the corners that occur in the Tresca form and their complete absence in the Mises form.

Two basic questions are immediately apparent:

Which procedure is better grounded, calibrating on T or calibrating on S?
Which criterion is more physically relevant, Mises or Tresca?

The steps of reasoning used here to answer these two questions are as follows:

Calibrating on S might seem more logical because yielding is caused by distortional not dilatational states in ductile materials and distortion more nearly and easily associates with shear stress rather than with uniaxial tensile (or compressive) stress.
However, shear stress involves only one parameter and that does not naturally generalize to a two parameter form which is necessary for non-perfectly ductile materials. On the other hand, T=C naturally and automatically generalizes to T and C (T≠C) in the more general cases. So T and C, not S, is the natural combination that converges to T=C for a one parameter form. Case II, calibrating on S, is accordingly rejected.
With calibration by T, giving Case I, there is still the choice between the Mises and Tresca forms. Mises is smooth, while Tresca has corners. At the crystal level (single grain) yielding does associate with dislocation movement on slip planes. This is caused by shear stress on the slip system (resolved shear stress). It would be tempting to say that this justifies and validates the Tresca criterion. But that is only part of the “story”. The condition of isotropy implies and applies to polycrystalline aggregates with the individual crystals taking all possible orientations. Dislocation induced plastic flow occurs over many slip systems. Furthermore, dislocation pile-up occurs at the grain boundaries. The vastly more complex behavior at the aggregate level compared with the crystal level must involve averaging over a wide variety of physical conditions and effects. This averaging has a smoothing effect that is much more supportive of the smooth Mises criterion than of the non-smooth Tresca form.
Conclusions 2 and 3 support and justify using the Mises (not Tresca) criterion for very ductile materials and calibrating on T (not S).

Further relevant background considerations are as follows. Tresca did do testing of metals that at the time seemed to support the maximum shear stress criterion. But that testing was superseded by the later excruciatingly careful testing performed by Taylor and Quinney and as shown in Section VI. The Taylor, Quinney results support the Mises criterion.

All T=C materials are metallic, polycrystalline aggregates. It is necessary to do orientation averaging to get the effective isotropic moduli properties. It is a parallel and consistent circumstance that orientational averaging must also be done to get the strength for polycrystalline aggregates. Mises (1) is consistent with this while Tresca (3) is not. Infact, Mises (1) is a composition or a type of average of the three separate criteria in (3), Tresca.

The non-smooth behavior evinced by the Tresca criterion usually associates with the competition of failure modes such as with a ductile flow mode and a brittle fracture mode. But those competitive effects are not present with ductile materials. Now consider a true 2-D type of continuum to see how it behaves. This is not plane stress or plane strain which are still 3-D behaviors. In this truly 2-D case it is found that a maximum shear stress criterion (Tresca) and a maximum distortional energy criterion (Mises) are identical, both giving smooth behaviors with continuous first derivatives Then in going to 3-D the Mises form continues this smooth behavior but the Tresca form brings in corners. The Tresca behavior in 3-D is an artifact of describing the maximum shear stresses in the three principal coordinate planes. This ignores the effects that occur at smaller scales in polycrystalline aggregates, and the averaging necessary to reach macroscopic behavior.

Even though the maximum difference between the Mises and Tresca criteria is only about 15% this difference represents a systemic error (divergence) on the part of the Tresca criterion and it should not be used for any isotropic materials, even for ductile metals. It is inappropriate to place the Tresca criterion on the same level as the Mises criterion, as is done in most tutorial works. The Tresca criterion only merits a historical reference. This is consistent with the fact that the Tresca criterion is the limiting case of the two parameter Coulomb-Mohr criterion which itself is only of historical interest. As discussed in Section VI the Mises criterion is the limiting case of a viable, completely general, modern failure criterion. Despite its restrictions, the Mises criterion is indeed a classical result.