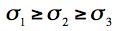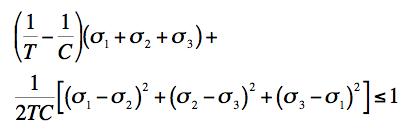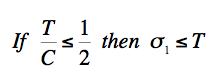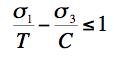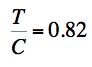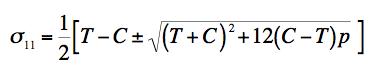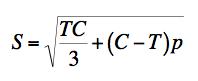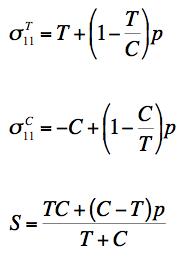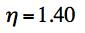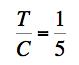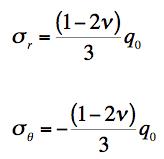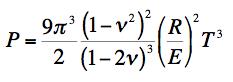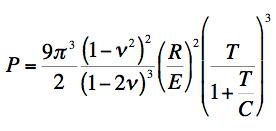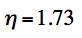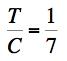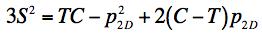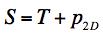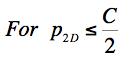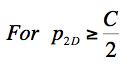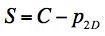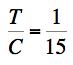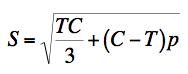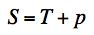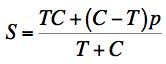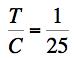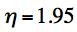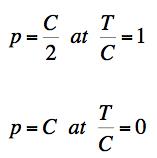Richard M. Christensen |
||
Failure Theory Applications |
|||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||
Now some examples of applications will be given. The purpose is not to evaluate and compare with data, that is covered in Section VI. Rather, the intention is to show the extraordinarily broad range and vitality of failure theory applications. All ductile metals are at or very near the strength ratio T/C=1, but all other materials classes such as polymers, ceramics, glasses, and geological materials have broad ranges of T/C’s. Examples from the various materials classes will be used with particular but realistic values of T/C in each case. These examples will range from very ductile polymers to extremely brittle geological materials. There is no need to cover ductile metals in the examples. They have been exhaustively treated in many places for a very long time. The Coulomb-Mohr failure theory was completely discredited by von Karman and by Böker not long after Mohr finished its development. That situation has been revisited and re-evaluated in Section VI, with the same end result. Still, it is useful to show Coulomb-Mohr results here in the examples in order to compare it with and calibrate the new, comprehensive failure theory. General The general, isotropic material failure criteria will be stated in principal stress space. The principal stresses will be taken to be ordered as
The failure theory treated here is given by two coordinated but independent criteria:
POLYNOMIAL INVARIANTS FAILURE CRITERION
and COORDINATED FRACTURE CRITERION
The coordination refers to the physical basis for the inception of the fracture criterion at T/C=1/2. This is a necessary and integral part of the failure theory, see Sections II and VI. The two failure mechanisms are competitive, whichever one gives the lesser allowable stress is controlling. In the examples these two criteria will be referred to as the Failure Criterion and Fracture Criterion respectively. The Coulomb-Mohr (Mohr-Coulomb) criterion is: COULOMB-MOHR FAILURE CRITERION
In the examples this will be referenced as the C-M Criterion.
Example 1, Very Ductile Polymer, The problem is that of the strength behavior of a very ductile, semi-crystalline polymer, polypropylene, under superimposed pressure. Polypropylene (and polyethylene) are very large volume, commodity plastics with a large variety of uses and applications. Although these materials have rather low stiffness and strength it is their ductility and toughness that enables most applications. In the present example, the uniaxial strengths are from Pae [1] at
The strength ratio T/C=0.82 denotes a very ductile behavior. This then could suggest that the Mises criterion would suffice for describing the failure characteristics. The main purpose of this example is to show just how wrong that casual assumption would be. For the material under pressure p the governing failure criteria are given by
FAILURE CRITERION
Of course the Mises criterion is unaffected by pressure. The pressure testing data, also from Pae [1], are at 1 kBar pressure = 101.4 MPa, which is about twice the compressive strength of the material. The data and predictions for the strengths under pressure are given by
It should be noted that the original data were given in psi units to two significant figures. The Mises criterion is calibrated by the tensile strength, as is conventional. The total square errors for the properties predictions compared with the data are given by Failure Criterion 5.5% error Mises Criterion 45.5% error It is seen that the worst of the three predictions by the Mises criterion is for uniaxial compression, and it differs from the data by a factor of 2.0. Incidentally, the total square error for the predictions from the C-M Criterion is 15.4%.
Example 2, Brittle Polymer, This example is similar to that of Example 1 but for a different material type that moves a little more toward the brittle end of the scale. Specifically, the material type is typified by that of PMMA, which is a transparent, rather brittle thermoplastic, widely used as an inexpensive replacement for glass, and often used in model experiments, especially for dynamic crack propagation. Although as a plastic it is considered as brittle, its strength ratio T/C ≅ 1/2 places it as intermediate on the overall scale for all materials. The uniaxial and shear Failure Criterion under pressure are the same as those given in Example 1 and the strengths for the C-M Criterion under pressure are given by C-M CRITERION
It is interesting to note that the C-M forms give a linear dependence on pressure p while the Failure Criterion forms in Example 1 give a square root dependence on p. The strengths at T/C=1/2 and for pressure p=2C (which is about the same pressure ratio in Example 1) are given by
The greatest difference between these is for uniaxial compressive strength at a factor of
Thus even at a reasonable pressure of p=2C these polymers show a wide difference between the two predictions. The differences widen even further at larger pressures for all three strengths. Furthermore, the effect of the pressure has a very strengthening effect on the strengths themselves.
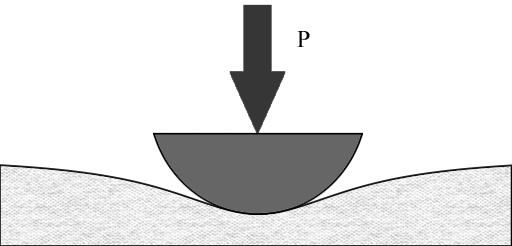
Example 3, Glass, The problem is that of pushing a curved indenter into an elastic but brittle material such as a glass or ceramic. This is the classical Hertz contact problem,
If the material were a ductile metal, the yielding would begin straight under the indenter, but at some depth. The interest here is with glass, and finding the location of its initial failure, and finding the load at which failure occurs. Take the indenter to be rigid and spherical of radius R. It is found that for the properties (Poisson’s ratio) of the brittle material of the half space, both failure criteria maximize at the edge of the contact zone. At this point the surface tractions vanish, and the in-plane stresses are
where q0 is the maximum pressure immediately under the indenter and on its center-line. The present failure criterion is controlled by the fracture form, and the analysis of the problem gives the force P acting on the indenter at failure as
FRACTURE CRITERION
C-M CRITERION
For T/C=1/5, which corresponds to a high quality glass such as S-glass, the two predictions of the load at failure differ by a factor of
Timoshenko and Goodier [2] note that many indentation experiments on glass have verified this location for the failure. Infact, it even goes back to the original experiments of Hertz.
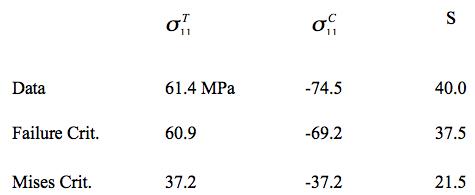
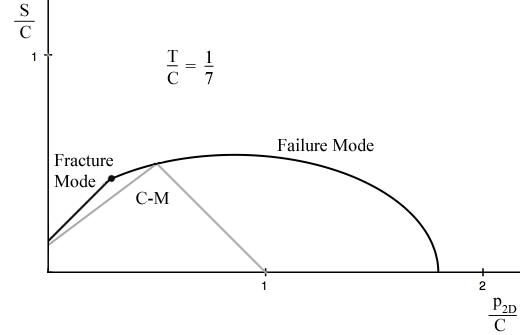
Example 4, Ceramic, In this example the effect of a two dimensional pressure upon the shear strength will be examined. The material of application will be for a typical ceramic. Ceramics function poorly under tensile stress states although they are very useful under combinations of shear stress and compression. Consider a thin layer of a ceramic as a heat shield and subject to pressure in its plane along with shear stress. In contrast to Example 2, here both the Failure Criterion and the Fracture Criterion will be found to play a role. The two dimensional pressure σ11= σ22 = -p2D, σ33 = 0 will be taken in the same plane as the shear stress σ12, having strength S. The governing criteria are FAILURE CRITERION
FRACTURE CRITERION
C-M CRITERION
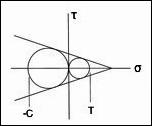
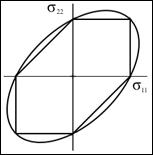
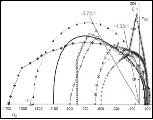
At T/C=1/7, the failure envelopes are as shown below
The shortcoming of the C-M Criterion in part relates to the fact that it does not account for the intermediate principal stress, σ2, in its formulation.
Example 5, Mineral, This problem is motivated by drilling through hard rock in exploration for water or hydrocarbons. The drill bit causes an intense local state of stress that is primarily composed of shear stress under pressure. The difference between this example and Example 4 is that here the pressure is three dimensional, p, rather than two dimensional pressure. The governing failure criteria are FAILURE CRITERION
FRACTURE CRITERION
C-M CRITERION
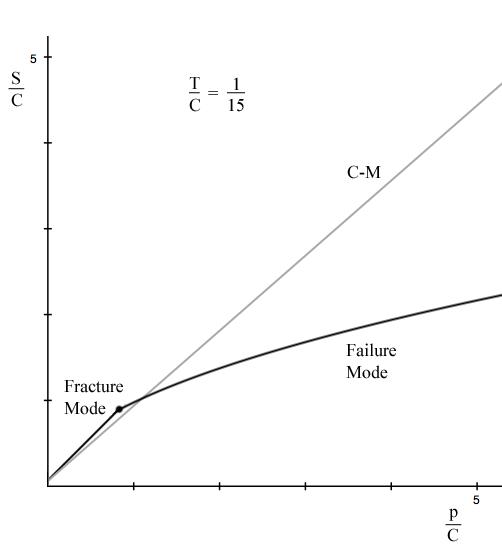
The plot of S versus p is given by
There is seen to be a major difference in behavior for three dimensional pressure from that that occurred in Example 4 with two dimensional pressure. In this example the C-M Criterion is mostly unconservative relative to the present failure criterion, whereas in Example 4 it was conservative. The present example is much like that in Section VI where the test data for dolomite were found to bifurcate away from the fracture mode and follow the failure mode as pressure increases, rather than following the straight line projection of C-M.
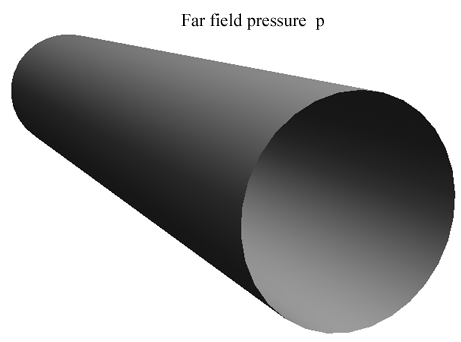
Example 6, Geo-Material, This is the problem of a tunnel buried under a large overburden, or equivalently a cylindrical cavity under far field hydrostatic pressure.
The tunnel is of radius “a” and the failure is found to always occur on that surface. The Fracture Criterion does not enter this problem and the other criteria are given by
FAILURE CRITERION
C-M CRITERION
At a geo-material value of T/C=1/25 the Failure Criterion gives
At this T/C the two criteria differ by a factor of
From the solution for the Failure Criterion it superficially appears that the tunnel can support a greater pressure at T/C=0 than it can at T/C=1
This nondimensionalized behavior is not only reasonable, it is necessary. The mean normal stress has no effect on the strength at T/C=1 but for lesser values of T/C a compressive mean normal stress does have a strengthening effect. Also, it must be remembered that as the material T/C diminishes, the absolute values for T and C individually also diminish greatly due to the greater degree of damage that exists at smaller T/C’s over the spectrum of materials.
As seen from the examples, sometimes the C-M Criterion is conservative and sometimes unconservative relative to the present theory. It is not possible to state a general rule that covers all cases. However, when all the principal stresses are predominately positive or all predominately negative then it can be shown that the C-M Criterion is always unconservative, sometimes extremely so, as in Example 5. In contrast, the present failure theory relies upon its physical development with experimental verification for realistic applications. Future world-wide applications will be designed to integrate the basic function with life cycle costs, efficiency, safety, durability and possibly several other requirements. Specific applications that reflect the new approach likely will include green aircraft, efficient automobiles, durable wind turbines, and many other emerging technologies. Such applications as these will in many cases necessitate the development and qualification of entirely new materials. The opportunity to understand and apply materials failure theory to these problems is completely open and the incentive is considerable.
References
|
|||||||||||||||||||||||||||||||||||||||||||||
Recent Additons |
|||||||||||||||||||||||||||||||||||||||||||||
Key Junctures |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
General Matters |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
Can Atomic/Nano Scale |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||
Copyright© 2019 |
|||||||||||||||||||||||||||||||||||||||||||||